1. 数一数

点数法：数数时，要按一定的顺序来数，从1开始，数到最后一个事物所对应的是几，即最后数到几，事物的总数就是几。

数图中物体的数量时，要按一定的顺序来数，比如可以按从上到下，从左到右，从远到近等顺序来数数。

各种事物的数量都可以用一个数表示。比如1面红旗，2本书，3块面包等。但有时数字也可以表示多个数量的同一种事物分成的几类或几个整体。比如1群大雁，4个小组的学生，3袋糖果等。

2. 比多少

同样多：两种事物一一对应后都没有剩余，就说这两种事物的数量同样多。

比多少：两种事物一一对应后，如果一种事物有剩余，那么有剩余的那种事物就多，没有剩余的那种事物就少。

描述物体多或少时，不能只说谁多谁少，应该说“谁比谁多”或“谁比谁少”。

小提示：求一个物体 比 另一个物体 “ 多几 ”或“ 少几 ”的问题，有两种解题方法：①“一 一对应”连线，然后把多地圈起来，数数圈起来的有几个就是多几个。②数一数两种物体各有几个以后作小记号，最后用大数减小数。如：

第二单元《位置》知识点

1. 认识上、下

上是指位置在高处的，与下相对；下是指位置在低处的，与上相对。

2. 判断上、下位置关系的方法：

首先确定参照物，再确定所描述的物体是在参照物的上面，还是在参照物的下面。

上、下是两个具有相对关系的方位，两者相互依存，不能单独存在。不能单独说某物体在上面或下面，应说某物体在另一物体的上面或下面。

3. 认识前、后

一般面对的方向是前，背对的方向是后。

4. 判断前、后位置关系的方法：

以参照物为标准，参照物面向的方向是前，背对的方向是后。

前、后是两个具有相对关系的方位，两者相互依存，不能单独存在。不能单独说某物体在前面或后面，应说某物体在另一物体的前面或后面。

同一物体相对于不同的参照物，上、下、前、后的位置关系会发生变化。因此，确定两个以上物体的上、下、前、后位置关系时，要找准参照物，选择的参照物不同，相对的上、下、前、后位置关系会发生变化。

5. 认识左、右

左手所在的一边是左边，右手所在的一边是右边。

要点提示：

（1）在确定左右时，一般以观察者的左右为准，当观察者身体方向发生变化时，左边和右边也发生相应的变化。但始终和左手、右手所在的一边保持一致。

（2）要确定图中人物的左、右位置关系，可以把自己假设为图中人物来判断。

第三单元《1-5的认识和加减法》知识点

一、 1--5的认识

1、1—5各数的含义：每个数都可以表示不同物体的数量。有几个物体就用几来表示。

2、1—5各数的数序

从前往后数：1、2、3、4、5.

从后往前数：5、4、3、2、1.

3、1—5各数的写法：根据每个数字的形状，按数字在田字格中的位置，认真、工整地进行书写。

二、比大小

1、前面的数等于后面的数，用“=”表示，即3=3，读作3等于3。前面的数大于后面的数，用“＞”表示，即3＞2，读作3大于2。前面的数小于后面的数，用“＜”表示，即3＜4，读作3小于4。

2、填“＞”或“＜”时，开口对大数，尖角对小数。

三、第几

1、确定物体的排列顺序时，先确定数数的方向，然后从1开始点数，数到几，它的顺序就是“第几”。第几指的是其中的某一个。

2、区分“几个”和“第几”

“几个”表示物体的多少，而“第几”只表示其中的一个物体。

四、分与合

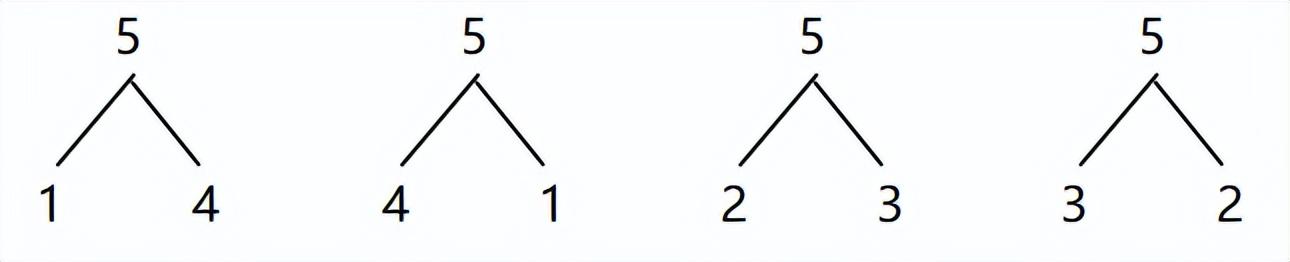
数的组成：一个数（1除外）分成几和几，先把这个数分成1和几，依次分到几和1为止。例如：5的组成有1和4,2和3,3和2,4和1.

把一个数分成几和几时，要有序地进行分解，防止重复或遗漏。

2~5的分分合合

（1）2的组成：

（2）3的组成：

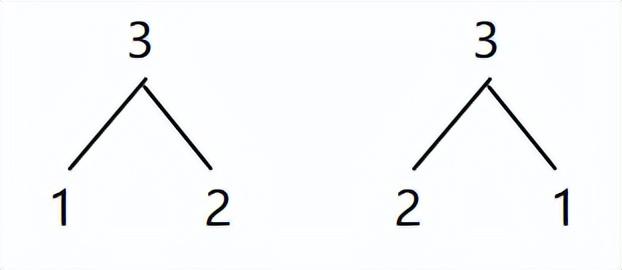
（3）4的组成：

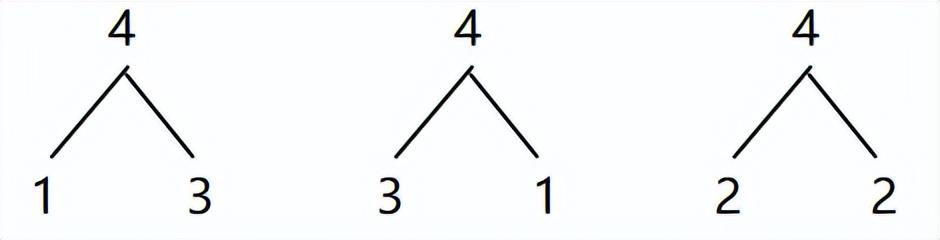
（4）5的组成：

五、加法

1、加法的含义：把两部分合在一起，求一共有多少，用加法计算。

2、加法的计算方法：计算5以内数的加法，可以采用点数、接着数、数的组成等方法。其中用数的组成计算是最常用的方法。

六、减法

1、减法的含义：从总数里去掉（减掉）一部分，求还剩多少用减法计算。

2、减法的计算方法：计算减法时，可以用倒着数、数的分成、想加算减的方法来计算。

七、0

1、0的意义：0表示一个物体也没有，也表示起点。

2、0的读法：0读作：零

3、0的写法：写0时，要从上到下，从左到右，起笔处和收笔处要相连，并且要写圆滑，不能有棱角。

4、0的加、减法：任何数与0相加都得这个数，任何数与0相减都得这个数，相同的两个数相减等于0.

如：0+8=8 9-0=9 4-4=0

第四单元《认识图形》知识点

一、立体图形

1、长方体

长方体是长长的，有6个平平的面，有些面是一样的，有些面是不一样，长方体相对面相等，用它可以画出长方形。平时见到的火柴盒、文具盒都是长方体。

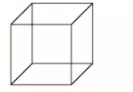
2、正方体

正方体四四方方的，它也有6个平平的面，它的边也是直直的。而且它的棱都是一样长，每个面都一样大，无论怎么平放在桌子上，它的高矮都是一样的，用它可以画出正方形。魔方就是正方体。

3、圆柱体

圆柱就像一根柱子。它有上下两个圆圆的面，而且大小一样，用它可以画出圆形；另一个面是弯曲的，我们把弯曲的面放在桌子上就可以滚动它。

4、球

圆圆的，可以滚来滚去的就是球。平时玩的皮球、篮球、踢得足球都是球。

5、立体图形的拼组

（1）用长方体或正方体可以拼组成不同的立体图形。

（2）用小的圆柱可以拼组成更大的圆柱。

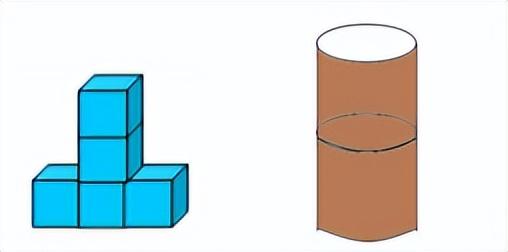
练习：

小提示：

①数图形时，要按照一定的顺序来数，最好是按 “从左到右、从上到下”或“从上到下、从左到右” 的顺序来数比较不容易出错。而且要细心多数几遍，确定没有漏数或多数了才填上答案。

②图形与分类结合的题目，要注意如果都是平面图形或都是立体图形就可按照形状来选，如果大部分是平面图形,只有一个是立体图形，那么该立体图形就是不同类的。

③一些容易混淆的图形要注意正确区分，如圆和球，正方体和正方形等。

1、数一数，填一填。

二、复习加、减法。

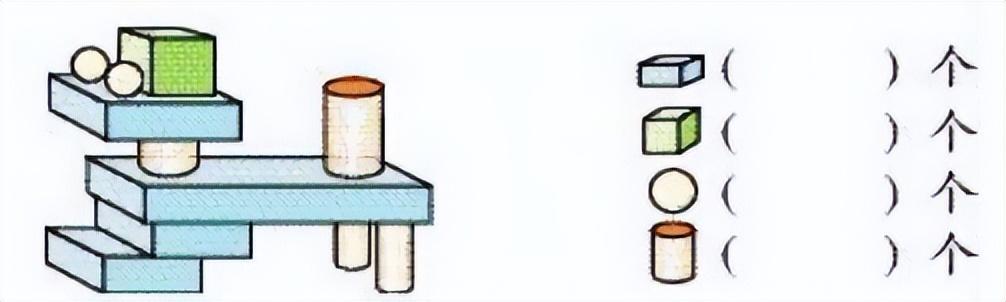
把两个数合并在一起用加法。加数+加数=和如：3+13=16中，3和13是加数，和是16。

从一个数里面去掉一部分求剩下的是多少用减法。被减数-减数=差如：19-6=13中，19是被减数，6是减数，差是13。

（一）熟记表内加法和减法的得数

（二）知道以下规律

1.加法

（1）两个数相加，保持得数不变：如果相加的这两个数有一个增大了，则另一个数就要减小，且一个数增大了多少，另一个数就要减少多少。

（2）两个数相加，其中的一个数不变，如果另一个数变化则得数也会发生变化，且加数变化了多少，结果就变化多少。

（3）两个数相加，交换它们的位置，得数不变。

2.减法

（1）一个数减去另一个数，保持减数不变：如果被减数增大，结果也增大且被减数增大多少，结果就增大多少；被减数减小，则结果也减小，且被减数减小多少，结果也减小多少。

（2）一个数减另一个数，保持被减数不变：如果减数增大，结果就减小，且减数增大了多少，结果就减小多少；如果减数减小，则结果增大，且减数减小了多少，结果就增大多少。

（3）一个数减另一个数，保持的数不变：被减数增大多少，减数就要增大多少；被减数减小多少，减数也要减小多少。

（三）整理与复习10以内的加减法

1 2 3 4 5 6 7 8 9 10

0+1 1+1 2+1 3+1 4+1 5+1 6+1 7+1 8+1 9+1

0+2 1+2 2+2 3+2 4+2 5+2 6+2 7+2 8+2

0+3 1+3 2+3 3+3 4+3 5+3 6+3 7+3

0+4 1+4 2+4 3+4 4+4 5+4 6+4

0+5 1+5 2+5 3+5 4+5 5+5

0+6 1+6 2+6 3+6 4+6

0+7 1+7 2+7 3+7

0+8 1+8 2+8

0+9 1+9

0+10

1-2-3-4-5-6-7-8-9-10-

1-1 2-1 3-1 4-1 5-1 6-1 7-1 8-1 9-1 10-1

2-2 3-2 4-2 5-2 6-2 7-2 8-2 9-2 10-2

3-3 4 -3 5-3 6-3 7-3 8-3 9-3 10-3

4-4 5-4 6-4 7-4 8-4 9-4 10-4

5-5 6-5 7-5 8-5 9-5 10-5

6-6 7-6 8-6 9-6 10-6

7-7 8-7 9-7 10-7

8-8 9-8 10-8

9-9 10-9

10-10

第五单元《6-10的认识和加减法》知识点

1. 6~10的认识

（1）数数：根据事物的个数，可以用6~10各数来表示。

（2）10以内数的顺序（从前往后）：

0、1、2、3、4、5、6、7、8、9、10

（3）比较大小：按照数的顺序，后面的数总是比前面的数大，如：9>6，7<10。

（4）序数：即第几个，表示的是事物的次序。

（5）数的组成：一个数（0、1除外）可以由两个比它小的数组成，且组成的方法不唯一。如8由3和5组成，也可以是8由1和7组成。

2. 6~10的加减法

（1）10以内加减法的计算方法：可以根据数的组成来计算。

（2）一图四式：一幅图，由于观察的角度不同，通常可以写出两道加法算式和两道减法算式。如：

（3）带有“

”的题，要先明确问号的位置，确定是求总数还是求其中的一部分，再进行列式计算。如：

3. 连加、连减

（1）连加：从左往右依次计算。

（2）连减：从左往右依次计算。

4. 加减混合

从左往右依次计算，即先算出前面两个数相加或相减的结果，再用这个结果与第三个数相加或相减。

第六单元《11-20各数的认识》知识点

1、数数：

根据物体的个数，可以用11—20各数来表示。

2 数的顺序：

11—20各数的顺序是：11、12、13、14、15、16、17、18、19、20

3、比较大小：

可以根据数的顺序比较，后面的数总比前面的数大，或者利用数的组成进行比较。

4、11—20各数的组成：

都是由1个十和几个一组成的，20由2个十组成的。如：1个十和5个一组成15。

5、数位：

从右边起第一位是个位，第二位是十位。

6、11—20各数的读法：

从高位读起，十位上是几就读几十，个位上是几就读几。20的读法，20的读作：二十。

7、写数：

写数时，对照数位写，有1个十就在十位上写1，有2个十就在十位上写2.有几个一，就在个位上写几，个位上一个单位也没有，就写0占位。

8、十加几、十几加几与相应的减法

（1）、10加几和相应的减法的计算方法：10加几得十几，十几减几得十，十几减十得几。

如：10+5=15 17-7=10 18-10=8

（2）、十几加几和相应的减法的计算方法：计算十几加几和相应的减法时，可以利用数的组成来计算，也可以把个位上的数相加或相减，再加整十数。

（3）、加减法的各部分名称：

在加法算式中，加号前面和后面的数叫加数，等号后面的数叫和。

在减法算式中，减号前面的数叫被减数，减号后面的数叫减数，等号后面的数叫差。

9、解决问题

求两个数之间有几个数，可以用数数法，也可以用画图法。还可以用计算法（用大数减小数再减1的方法来计算）。

第七单元《认识钟表》知识点

1、认识钟面

钟面：钟面上有12个数，有时针和分针。

分针：钟面上又细又长的指针叫分针。

时针：钟面上又粗又短的指针叫时针。

2、钟表的种类：

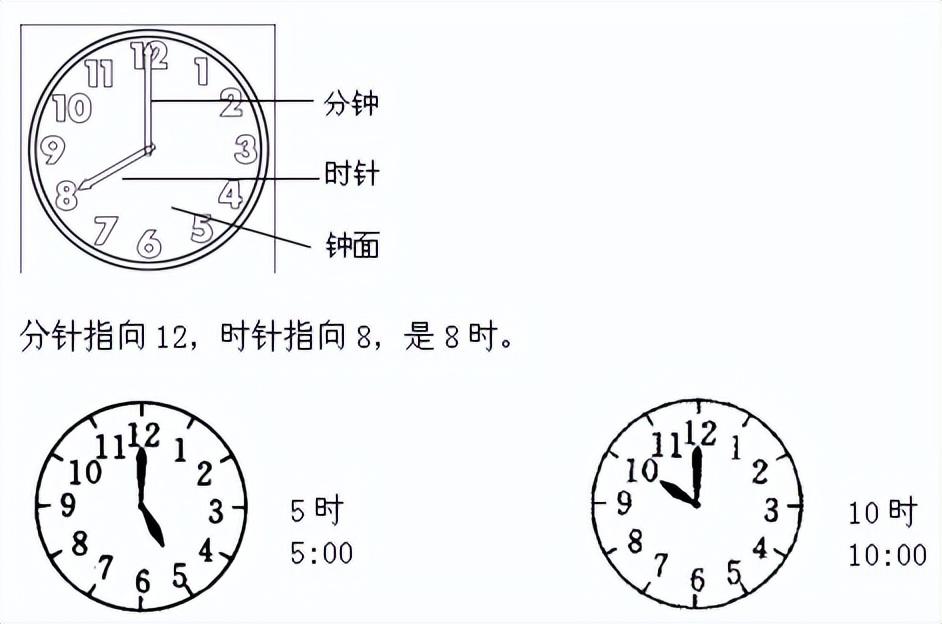
日常生活中的钟表一般分两种，一种：挂钟，钟面上有12个数，分针和时针。另一种：电子表，表面上有两个点“：”，“：”的左边和右边都有数字。

3、认识整时：

分针指向12，时针指向几时就是几时；电子表上，“：”的右边是“00”时表示整时，“：”的左边是几就是几时。

4、整时的写法：

整式的写法有两种：写成几时或电子表数字的形式。如：8时或8:00

第八单元《20以内的进位加法》知识点

1.掌握20以内进位加法的计算方法---“凑十法”“凑小数，拆大数”

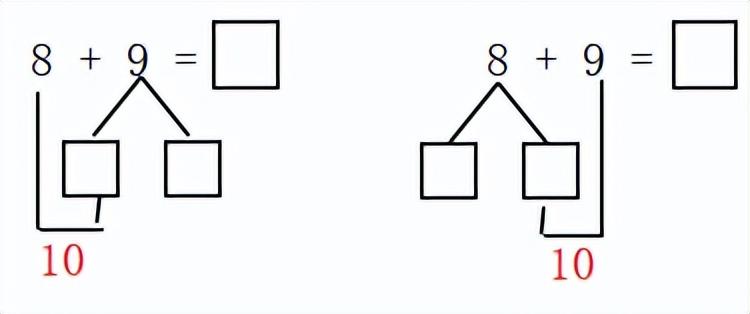
（1）9加几计算方法：计算9加几的进位加法，可以采用“点数”“接着数”“凑十法”等方法进行计算，其中“凑十法”比较简便。

利用“凑十法”计算9加几时，把9凑成10需要1，就把较小数拆成1和几，10加几就得十几。

如：

先把4分成1和3，然后1和9凑成10,10加3等于13。

（2）8、7、6加几的计算方法：a、点数；b、接着数；c、凑十法。可以“拆大数、凑小数”，也可以“拆小数、凑大数”。如：8+7（8+2=10,7可以分成2和5，10+5=15）

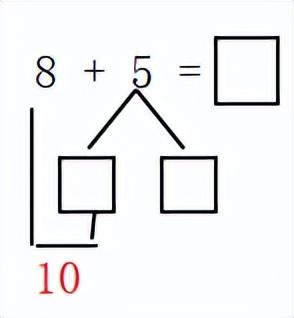
先把5分成（ ）和（ ），然后（ ）和8凑成10，10加（ ）等于（ ）。

（3）5、4、3、2加几的计算方法：a、“拆大数、凑小数”。b、“拆小数、凑大数”。

将小数凑成10，然后再计算。如：3+9（3+7=10,9可以分成7和2,10+2=12）

“凑大数，拆小数”，将大数凑成10，然后再计算。

注意：孩子喜欢和熟悉的方法才是最佳方法而且只掌握一种就可以了。

2.20以内不进位加法和不退位减法：

11+6（个位相加，1+6=7）

11+6=1715-3（个位上够减，5-3=2）

15-3=12

3、加强进位和不进位、及不退位的训练。

4、看图列式解题时候，要利用图中已知条件正确列式。

常用的关系有：

（1）部分数+部分数=总数

（2）总数-部分数=另一个部分数

（3）大数-小数=相差数（谁比谁多几，或谁比谁少几）

（4）原有-借出=剩下（用了多少，求还剩多少时用）

5、解决问题

（1）解决问题时，可以从不同的角度观察、分析、从而找到不同的解题方法。

（2）求总数的实际问题，用加法计算。